Теория о бесконечных обезьянах

Страшно люблю разного рода абстрактные теории и мысленные эксперименты, существующие исключительно в гипотетическом поле и слабопроверяемые в реальной жизни. Одной из таких теорий является теория о бесконечных обезьянах, предполагающая ситуацию, в которой бесконечное количество обезьян с печатными машинками за бесконечное количество времени — рано или поздно могут напечатать любой заданный наперёд текст. К примеру, «Войну и Мир» Толстого или какую-либо из пьес Шекспира.

К сожалению, конечно, данная теория останется навсегда теорией. Ввиду сложности доказательной базы. Согласитесь, весьма трудно где-то достать бесконечное количество печатных машинок, обезьян и бесконечное время следить за всем этим зоопарком. Но данная теория ложится в индуктивную плоскость доказательств и, посему, можно слегка уменьшить сложность — отмасштабировав задачу в сторону уменьшения, при этом не потеряв в проверяемости.

Мы напишем компьютерную программу. Очень простую, но в то же время — решающую нашу задачу за какое-то плюс-минус конечное время. Мы создадим свою собственную обезьяну. Всего одну, но очень-очень быструю.

Словарь.

Очень важен выбор «заданного наперёд» произведения. Важен и язык этого текста. Я решил взять первый абзац произведения Льва Толстого «Анна Каренина«. Без какой-либо конкретной причины, просто захотелось 🙂

Выбор языка стратегически намного более важная задача, чем выбор самого текста. В русском алфавите 32 буквы, в английском 26 букв. Используя теорию вероятностей нам не составляет труда понять, что пятибуквенное слово на русском языке сгенерировать случайным образом на порядок сложнее, чем на английском.

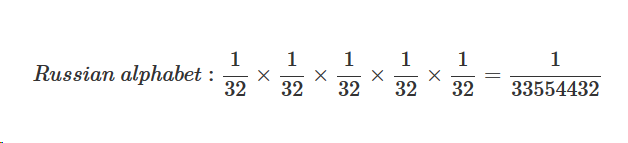
Фактически при изменении базы словаря символов до 26 с 32 (на 6 меньше букв) мы получаем выгоду в 3 раза, соответственно, время затраченное на порядок меньшее. Английский алфавит:

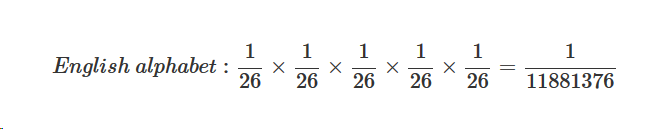
Можно было бы, конечно, воспользоваться ещё более скромным языком — Ротокас (группа т.н. папуасских языков) в алфавите которого есть только 12 букв. И вероятность подобрать пятибуквенное слово составила бы 1 к 248 832, что более чем приемлемо и терпимо. Проблема заключается в том, что средняя длина слов в этом языке просто неприлично огромная и мы аннигилируем всю выгоду банально потому, что наш текст безмерно увеличится в объёме символов.

Важно: 1/26 и 1/32 это вероятность найти букву. В случае, когда в нашем тексте используется разный регистр букв (заглавная и строчная) — наш делитель-знаменатель увеличивается вдвое. В случае, когда в базу словаря добавляются знаки препинания и пунктуации, а также цифры — сильно усложняет наш эксперимент во временной шкале. Здесь мы также пойдём на упрощение — откажемся от любых символов, кроме строчных букв и, соответственно, приведём весь текст в lowercase.

Алгоритм.

Итак, английский. Теперь необходимо подумать о самом алгоритме. Теория умалчивает о подходах и реализациях, оставляя решение данных требований на участь экспериментатора. Чем я с удовольствием и воспользуюсь (самым наглым образом).

Первым наперво стоит указать, что генератор случайных цифр символов из обезьяны (ровным счётом, как и из человека) никакой. Очень плохой ГСЧ. Очень сложно получить равномерное статистическое распределение между нажимаемыми клавишами. Это означает, что вероятность 1/26 является вероятностью в «идеальном мире«, который, как известно, бывает только на бумажке. Также очень сильно хромает скорость такого набора. Поэтому здесь мы также идём на осознанное упрощение — мы воспользуемся ГСЧ, который нам предоставляет наши современные реалии.

Существует несколько способов генерировать текст случайным образом:

• по-символьно, когда мы ожидаем, что обезьяна случайно брякнет конкретную необходимую нам букву и игнорируем все остальные «неудачные» нажатия. Вероятность набить весь текст при таком подходе реален даже в эксперименте с живыми обезьянами (при небольшом заданном тексте);
• слово целиком — считаем успешным лишь тот случай, когда обезьяна чередой случайных нажатий вбила слово. Становится сложнее экспоненциально;
• весь текст целиком — когда весь текст обезьяной вбивается от начала и до конца без ошибок. Сложность также растёт по экспоненте.

Первый пункт мы не рассматриваем за его неинтересность. Последний тоже, т.к. скорее всего времени, отведённого на нашу вселенную — не хватит на такой эксперимент. Центральный вариант кажется рабочим. Но и он требует уточнения. Многие слова в книге повторяются. И тут мы также пойдём на упрощение (на этот раз финальное) — мы будем подбирать только уникальные слова, чтобы тысячи раз не тратить время на союзы, предлоги и другие служебные части речи; туда же попадают имена нарицательные и все слова, повторяемые не единожды.

Пишем код.

Как всегда, это будет консольное приложение. Маленькое. Мы не будем писать мультипоточное приложение, расплодив обезьян с их машинками. Для нашей задачи вполне хватит основного потока. Итак, создадим проект MonkeyInfinity и добавим следующие константы и переменные в Program.cs:

const string FILE_PATH = @"d:\Data\text.txt";

private static char[] TRIM_CHARS = new char[] { '!', '@', '#', '
, '%', '^', '&', '*', '(', ')', '-', '+', '=', '_', '\\', '|', '/', '.', ',', '<', '>', '`', ';', ':', ' ', '\r', '\n' };

private static Random _random;

Здесь всё просто — мы инициализируем текстовую константу с указанием файла нашего текста, массив символов для обрезания строк и экземпляр класса нашего ГСЧ. Теперь, давайте, получим сам текст и приведём его к lowercase виду:

static string GetText()
{
	string content = File.ReadAllText(FILE_PATH);
	content = content.ToLower();
	return content;
}

Следующий шаг — получить словарь букв для подбора. Мы должны использовать в нашем генераторе только уникальные символы; также игнорировать любые не буквенные символы. Можно было бы, конечно, реализовать при помощи char.IsLetter(), но я осознанно оставил возможность регулировать нужные нам символы.

static List<char> GetLettersBase(string text){
	List<char> result = new List<char>();
	foreach(char c in text.ToCharArray())
	{
		if(!TRIM_CHARS.Contains(c) && !result.Contains(c))
			result.Add(c);
	}
	return result;
}

Теперь, логично, получить словарь уникальных слов:

static List<string> GetWordsBase(string text)
{
	List<string> result = new List<string>();
	string[] split = text.Split(new char[] { ' ', '\r', '\n' }, StringSplitOptions.RemoveEmptyEntries);
	foreach(string c in split)
	{
		string tmp = TrimWord(c);
		if (!string.IsNullOrEmpty(tmp) && !result.Contains(tmp))
			result.Add(tmp);
	}
	return result;
}

static string TrimWord(string word)
{
	return word.Trim(TRIM_CHARS);
}

Итого, у нас есть все символы, необходимый набор клавиш нашей виртуальной печатной машинки и есть слова, которые мы ожидаем от обезьяны программы. Давайте попробуем что-то сгенерировать:

static string GetRandomWord(List<char> chars, int max)
{
	int c = _random.Next(1, max + 1);
	StringBuilder sb = new StringBuilder();
	for (int i = 0; i < c; i++)
		sb.Append(GetRandomChar(chars));
	return sb.ToString();
}

static char GetRandomChar(List<char> chars)
{
	return chars[_random.Next(0, chars.Count)];
}

Постепенно переходим к самому интересному — реализация механизма подбора слов. Данный метод я назвал Run, как основную задачу нашей маленькой программки. Здесь же я засекаю время старта подбора и время завершения. Внутри тела метода есть цикл, работающий до тех пор, пока мы не подберём все слова. В случае подбора слова — сбрасываем в консоль соответственные данные. Итак, Run:

static void Run(List<char> chars, List<string> words, int max)
{
	int c = 0;
	long it = 0;
	DateTime dt = DateTime.Now;
	Console.WriteLine("Start time: " + dt.ToString());
	List<string> result = new List<string>();
	do
	{
		string tmp = GetRandomWord(chars, max);
		if (words.Contains(tmp) && !result.Contains(tmp))
		{
			result.Add(tmp);
			c++;

			Console.WriteLine("Wow! Word: " + tmp + " (iteration: " + it + "). Ellapsed time: " + DateTime.Now.Subtract(dt).ToString() + ". Progress " + result.Count.ToString() + " from " + words.Count.ToString());
		}
		it++;
	}
	while (result.Count != words.Count);
	Console.WriteLine("End time: " + DateTime.Now.ToString());
	Console.WriteLine("Ellapsed time: " + DateTime.Now.Subtract(dt).ToString());
}

Когда готовы все кубики — осталось последнее. Метод Main(), наша точка входа и выхода. Нам нужно связать кубики в бизнес-логику и заставить программу работать — для этого реализуем наш метод, добавив в него небольшую статистику по самому большому и маленькому слову:

static void Main(string[] args)
{
	Console.Title = "Infinity Monkey";
	Console.WriteLine("Infinity Monkey");

	_random = new Random(DateTime.Now.Millisecond);
	string content = GetText();
	List<char> chars = GetLettersBase(content);
	List<string> words = GetWordsBase(content);
	string min = words.OrderBy(m => m.Length).FirstOrDefault();
	string max = words.OrderByDescending(m => m.Length).FirstOrDefault();

	Console.WriteLine("Text file: " + FILE_PATH);
	Console.WriteLine("Text length: " + content.Length.ToString() + "b.");
	Console.WriteLine("Chars count: " + chars.Count.ToString());
	Console.WriteLine("Words count: " + words.Count.ToString());
	Console.WriteLine("Min word length: " + min.Length.ToString() + " [" + min + "]");
	Console.WriteLine("Max word length: " + max.Length.ToString() + " [" + max + "]");

	Console.WriteLine();
	Console.WriteLine("Text:");
	Console.WriteLine(content);
	Console.WriteLine();

	Run(chars, words, max.Length);

	Console.Read();
}

Всё готово для проверки. Осталось подобрать текст. Для того, чтобы всё тщательно продебажить (вас то я уже лишил этой радости 🙂 ), я взял коротенькие английские пословицы. Сохранив в файле text.txt следующий текст: Every man has his price я впервые запустил программу. Мне кажется, что это хороший пример для старта — предложение с тремя трёхбуквенными и двумя пятибуквенными словами. Итак, барабанная дробь, запуск:

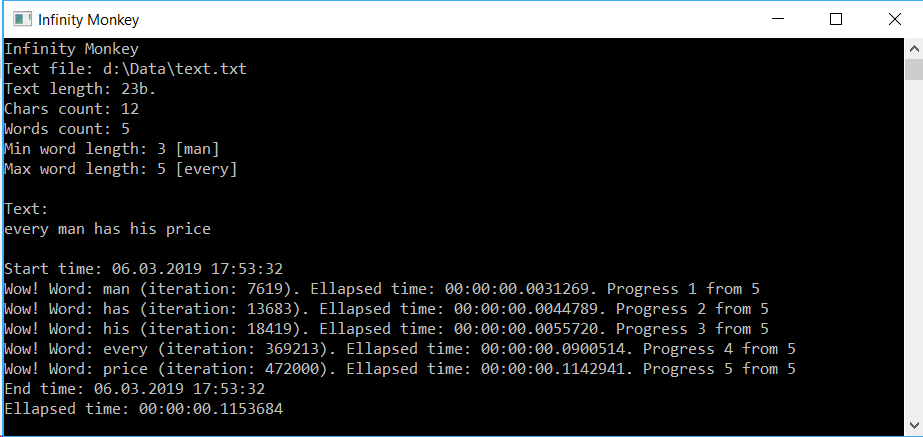
Как видно из лога, программе понадобилось 472000 итераций и около ~0.115 секунды для того, чтобы решить данную задачу. Ожидаемо, что трёхбуквенные слова были подобраны быстрее, чем слова из пяти букв. Хоть и на это понадобилось 18к итераций!

5-6 буквенные слова подбираются сравнительно быстро. Если практически на все слова из 5 букв уходит менее секунды, то на слова от 6 символов — рост времени наблюдается экспоненциальный. Число итераций зашкаливает — не думаю, что какая-либо уважающая себя обезьяна на такое пойдёт добровольно 🙂 На моём i7 процессоре с 24гб ОЗУ первый абзац Анны Каренины, состоящий из 117 уникальных английских слов (где самое длинное слово housekeeper 11 букв) подбирается уже неделю и были найдены только все 7-ми буквенные слова, несколько слов из 8 букв и одно из 9-ти. Не быстро, мягко говоря, но и не невозможно.

P.S. Код писался быстро и исключительно для локального использования. Там нет никаких SOLID принципов, потому что их там особо некуда притулить. Этот код не нужно воспринимать серьёзно. Да и оверхед там, где он не нужен — это тоже антипаттерн.

Особо чувствительный читатель возмутиться отсутствием проверок на наличие файла и хендлинга ошибок, но это всё было не нужно, т.к. то, что требовалось от программы — я получил.

Выводы.

Выводы, конечно, банальные, предсказуемые и ожидаемые. Теория имеет место быть, она валидна и проверяема в масштабе. Если теория подтверждается в идеальных искусственных условиях за очень короткое конечное время — нет оснований полагать, что в реальном мире мы также не придём к нужному результату. Спасибо индукции.

Да, бесконечное время. Да, скорее всего, мы не сможем самостоятельно дождаться конца этого эксперимента. Возможно, что и вселенная к этому моменту перестанет существовать. Но вероятность всё равно будет стремиться к единице, а это значит, что нам остаётся только лишь набраться терпения и просто немного подождать 🙂