Битовые маски и флаги в .NET C#
Сегодня хочу поднять очень полезную, но не самую популярную в последнее время тему — использование поразрядных операций над двоичными числами, работа с битовыми масками и, соответственно, флагами. По сути всё вышеперечисленное — это звенья одной цепи и истории: как прятать хранить несколько значений (т.н. флагов) в одной численной переменной, а также как именно и где это использовать. К сожалению, всё чаще наблюдаю, что много современных программистов из «нового поколения» не работают с данным типом представлений вообще и, что ещё хуже, практически не знакомы или не слышали об этой идее. Всё дело в том, что подход достаточно низкоуровневый и по сегодняшним меркам весьма не прост с позиции высокой точки входа. Надеюсь, что эта небольшая статья поможет вам понять, разобраться или же просто вспомнить этот важный битовый навык.
Перед тем как начать, хочется сделать небольшое вступление и напомнить, что все десятичные числа могут быть представлены в двоичном виде, в котором каждый разряд является минимальной и неделимой единицей информации — битом; т.е. такая маленькая коробочка, в которую можно положить либо ноль (ложь), либо единицу (правда). Только так и ничего другого. Как перевести число из десятичной в двоичную систему (или любую другую) в интернете написано масса информации и повторяться смысла нет. Это самый базовый и начальный курс computer science, школьная программа информатики. Поэтому я подразумеваю, что читатель уже умеет это делать. В конечном итоге из десятичного числа у вас должен получиться ряд из нулей и единиц. К примеру, для десятичного числа 91 ряд будет выглядеть примерно следующим образом (рисовал на планшете, авторское исполнение 🙂 но, я уверен, в этом есть некоторая определённая прелесть):
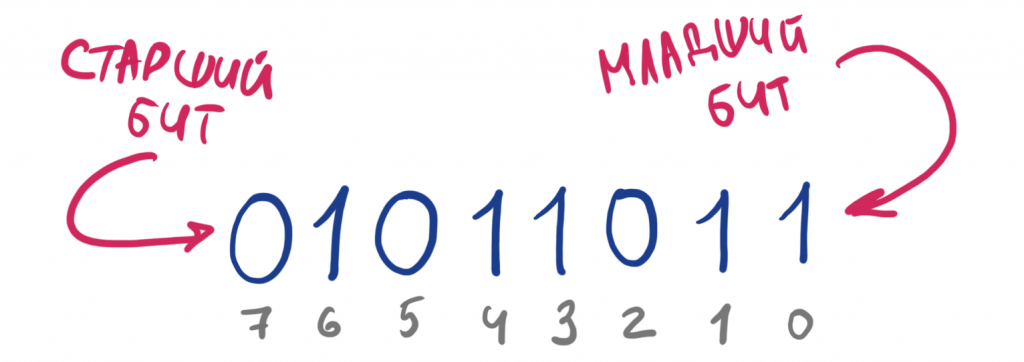
Теперь про саму идею — мы будем хранить одно или множество значений в одном числе (переменной), где каждый бит будет прикреплён к какому-либо заранее предетерминированному флагу\значению\смыслу. Возьмём, к примеру классическую задачу организации доступа юзера и примем, что у нас на сайте есть абстрактные группы, в которых есть следующие виды «допусков»: чтение статей, создание статей, удаление статей, чтение комментариев, написание комментариев, удаление комментариев, создание юзеров и блокировка юзеров. Всего 8 штук и это число я взял не случайно — именно столько бит в байте, а значит все возможные комбинации этих групп мы можем уместить всего-лишь в одном байте. Выглядит это следующий образом:

Или вот пример из личного опыта — совсем недавно занимался обработкой изображений и по долгу службы работал с CMYK системой цветов. По задаче мне необходимо было обрабатывать цветовые каналы отдельно друг от друга или же вместе. В любых комбинациях, соответственно, для CMYK это 15 всевозможных комбинаций. Подобное множество запрограммировать «просто и быстро» — не просто и не быстро 🙂 Но, если применить битовые маски, где, скажем, 4й бит это С, 3й бит — М, 2й — Y и 1й — K, всё становится на порядок легче и проще! Можно передавать всевозможные комбинации используя всего-лишь один байт (и то, займём там только половину «полезной площади»).
Таблица истинности
Итого, мы умеем переводить числа в двоичное представление. Теперь необходимо вспомнить таблицу истинности (хотя, конечно, это не про «вспомнить», а про элементарную логику, которая обычно выводится — ничего запоминать не нужно). О таблице, которая описывает все логические функции — какие аргументы поступают на входе, какая применяется операция и какой результат на выходе. Всё это в сокращённом виде (для базовых функций AND, OR, XOR) выглядит так:
| A | B | AND | OR | XOR |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Логические операторы
Как правило все вышеописанные логические функции представлены во всех языках программирования в том или ином виде и конкретно для «си-подобной» группы языков это, как правило, абсолютно всегда одинаковый синтаксис. Вы встретите это в C, С++, C#, PHP, JavaScript, Python и ещё много где. Это всё в некотором роде уже стало стандартом синтаксиса для битовых (bitwise) операций.
Оператор & для AND
Логическое И или же конъюнкция. Результатом работы данной логической операции является множество (т.к. на вход поступает два операнда из множеств нулей и единиц), вычисляемое по таблице истинности, т.е. если оба бита в текущем столбце строки являются единицами (или true), то возвращаем тоже единицу. Так проходим по всем элементам нашей строки.
Разберём пример — для строчки кода 111 & 222 ответ будет 78, т.к. 111 в десятичной системе это 01101111 в двоичной, а 222 — 11011110. Проходя каждый элемент и применяя поочерёдно логическую операцию AND мы получим 01001110 (единица там и только там, где в исходных битах обоих операндов были единицы), что является 78 в десятичной системе.
Вот ещё несколько примеров логического И (биты, которые «отработали» положительно я выделил жирным):
| dec | bin | AND | dec | bin | Result | dec | bin |
|---|---|---|---|---|---|---|---|
| 111 | 01101111 | & | 222 | 11011110 | = | 78 | 01001110 |
| 43 | 00101011 | & | 96 | 01100000 | = | 32 | 00100000 |
| 131 | 10000011 | & | 87 | 01010111 | = | 3 | 00000011 |
| 47 | 00101111 | & | 255 | 11111111 | = | 47 | 00101111 |
Оператор | для OR
Логическое ИЛИ или же дизъюнкция. Здесь, в отличии от AND, нам для «положительного» результата необходимо, чтобы хотя бы один из операндов равнялся единицы. Без разницы левый, правый или оба — возвращаем 1, в противном случае — 0. Как видно из таблицы истинности для логического ИЛИ мы почти всегда будет получать единицу, кроме случая, когда оба операнда слева и справа равны нулю.
Разберём пример (я буду рассматривать такие же числа во всех примерах, чтобы можно было понять\уловить разницу). 111 | 222 будет равняться 255, т.к. 01101111 ИЛИ 11011110 вернут все единицы 11111111 (у нас нет ни одного случая при котором было бы два ноля).
Также, как и в предыдущем примере, добавляю таблицу примером логического ИЛИ:
| dec | bin | OR | dec | bin | Result | dec | bin |
|---|---|---|---|---|---|---|---|
| 111 | 01101111 | | | 222 | 11011110 | = | 255 | 11111111 |
| 43 | 00101011 | | | 96 | 01100000 | = | 107 | 01101011 |
| 131 | 10000011 | | | 87 | 01010111 | = | 215 | 11010111 |
| 47 | 00101111 | | | 255 | 11111111 | = | 255 | 11111111 |
Оператор ^ для XOR
Исключающее ИЛИ или строгая дизъюнкция — моя любимая логическая операция, если, конечно, можно испытывать чувства к этому. Также известная как XOR или сложение по модулю 2, поразрядное дополнение, инвертирование по маске, жегалкинское сложение, логическое вычитание или логическая неравнозначность. Эта прекрасная операция вернёт вам единицу или true в том случае, если строго один (любой, но только один) операнд равен нулю.
Для нашего примера из чисел 111 ^ 222 ответом будет 177, потому что 01101111 XOR 11011110 даст 10110001
| dec | bin | XOR | dec | bin | Result | dec | bin |
|---|---|---|---|---|---|---|---|
| 111 | 01101111 | ^ | 222 | 11011110 | = | 177 | |
| 43 | 00101011 | ^ | 96 | 01100000 | = | 75 | 01001011 |
| 131 | 10000011 | ^ | 87 | 01010111 | = | 212 | 11010100 |
| 47 | 00101111 | ^ | 255 | 11111111 | = | 208 | 11010000 |
Оператор битового смещения (сдвига) влево <<
Битовый сдвиг влево — это перенос всех бит на одну позицию влево с потерей крайней левой (если речь идёт о процессорах, то, как правило, крайнее левое значение сохранение в регистр флага переноса) и добавлением одного нуля справа. Битовый сдвиг влево на 1 умножает число на 2, сдвиг на 2 — на 4 и т.д. К примеру, 13 << 1 даст 26, а 13 << 2 даст уже 52.
Оператор битового смещения (сдвига) вправо >>
Обратная операция левому сдвигу — битовый сдвиг вправо — сдвигает все биты вправо с потерей крайнего правого бита и добавлением одного нуля слева. Данный сдвиг — делит. К примеру, сдвиг на 1 делит число на 2, сдвиг на 2 — на 4 и т.д. 24 >> 1 — получим 12, а в случае 24 >> 2 — получим 6.
Оператор ~ для NOT
Самый простой оператор ~, работающий с одним операндом (т.е. унарная операция) — это логическое НЕ, которое инвертирует наши входные данные на противоположные (true на false и наоборот), т.е. если есть 1 — то возвращаем 0 и, соответственно, если 0 — то 1. Здесь без таблиц, всё более менее должно быть очевидно.
Есть только один ньюанс — инвертирование изменяет также знак числа. К примеру ~123 станет -124, т.к. первый разряд битового представления отвечает за знак числа — если там установлена единица, значит число отрицательное. Таким образом мы можем умножать числа на -1 путём инвертирования и прибавления 1: ~123+1. Этот способ называется дополнительный код (или two’s complement) — наиболее простой и эффективный вариант представления отрицательных чисел для компьютера.
Работа с битами
Вооружившись логическими операторами мы теперь имеем достаточно инструментария, чтобы устанавливать конкретные биты в нужные места, проверять их состояние, изменять или удалять. Но перед тем, как мы начнём производить манипуляции над битами, хочу напомнить вам ещё кое что — каждый разряд бита в двоичном представлении это ряд степени двойки, т.е. 2^n. Посмотрите, как единичка «двигается» по диагонали в зависимости от степени — именно так мы и будем «вычленять» или, наоборот, добавлять нужные нам флаги:
| n | dec | B7 | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 8 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 16 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 5 | 32 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6 | 64 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 128 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Теперь пример. Для того, чтобы заменить в числе 0b11110111 ноль на единицу, мы должны изменить четвёртый бит. Для этого необходимо применить логическое ИЛИ (OR) с десятичной восьмёркой (которая и несёт в себе этот самый бит — посмотрите в табличке), т.е. 0b11110111 | 0b1000 и мы получим 255, т.е. все восемь единиц 11111111.
Для того, чтобы убрать эту же единицу (т.е. совершить обратную операцию), мы должны воспользоваться исключающим ИЛИ (XOR): 0b11111111 ^ 0b1000 = 0b11110111.
Всего две эти операции дают нам возможность включать или отключать в нужном нам порядке нужные флаги. Как в массиве булевых переменных — зная индекс можно легко и просто получить доступ к значению: прочитать его или изменить. С разницей лишь в том, что занимать в память это будет на порядок меньше и оперирование такой структурой можно уместить в меньшее количество строк кода.
.NET C# пример перечисления
Давайте перенесём наш изначальный пример с ACL в код и создадим стандартый enum на языке C#:
[Flags]
public enum AccessLevels : uint
{
None = 0,
//Articles
READ_ARTICLES = 1,
WRITE_ARTICLES = 2,
DELETE_ARTICLES = 4,
//Comments
READ_COMMENTS = 8,
WRITE_COMMENTS = 16,
DELETE_COMMENTS = 32,
//Profiles
CREATE_PROFILES = 64,
BLOCK_PROFILES = 128,
ALL = ~None,
}
Данная структура позволяет нам создавать перечисления с типом uint и организовать примитивный и очень легковесный ACL (access control list), т.е. систему доступов. Обратите также внимание, что каждый бит у нас пронумерован согласно степени двойки и увеличивается в два раза для каждого последующего элемента. Также важно оставлять первый элемент None с значением нуля, т.к. по-умолчанию структура принимает значение 0 — это считается хорошей и правильной практикой. Последним элементом идёт ALL равный инверсией None (т.е. заполнены все биты, все возможные варианты значений).
Здесь же вы можете заметить, что все последующие элементы «привязаны» к значениям степени двойки (1, 2, 4, 8, 16, 32…) — это те самые биты, которые мы и будем «устанавливать». К слову, записывать эти значения можно разными способами:
//Left shift
[Flags]
public enum CMYK1 : uint
{
None = 0,
C = 1,
M = C << 1,
Y = M << 1,
K = Y << 1,
}
//HEX
[Flags]
public enum CMYK2 : uint
{
None = 0,
C = 0x1,
M = 0x2,
Y = 0x4,
K = 0x8,
}
//BIN
[Flags]
public enum CMYK3 : uint
{
None = 0,
C = 0b1,
M = 0b1_0,
Y = 0b1_00,
K = 0b1_000,
}
Обратите внимание на последний способ записи — очень удобно маркировать значения в бинарном представлении чисел просто отделяя дополнительными нулями.
Также над нашими перечислениями можно наблюдать атрибут Flags, который является индикатором того, что данные enum можно использовать для битовых операций. Этот флаг не обязательный и всё будет работать и без него, но в некоторых случаях форматирования и обработки он помогает сохранять целостность нашего представления. К примеру, для ToString форматирования:
//Если мы не указываем атрибут [Flags]:
AccessLevels level = AccessLevels.READ_ARTICLES | AccessLevels.WRITE_ARTICLES;
Console.WriteLine(level.ToString("G")); //В выводе консоли мы увидим лишь число '3' (битовое значение в десятичном представлении).
//Если мы указываем атрибут [Flags]
Console.WriteLine(level.ToString("G")); //Здесь вывод будет отличаться: 'READ_ARTICLES, WRITE_ARTICLES'.
В остальном Flags особо никак нам не помогает и даже не контролирует то, что мы можем ввести элемент НЕ из ряда степени двойки, а любой другой какой захотим — ошибки не будет.
.NET C# пример битовых манипуляций
Рассмотрим следующий пример. Для того, чтобы «разрешить» все операции на чтение, нам необходимо «нанизать» нужные доступы через ИЛИ, т.е. каждый элемент который начинается с строки READ_:
AccessLevels level = AccessLevels.READ_ARTICLES | AccessLevels.READ_COMMENTS; // или AccessLevels level = AccessLevels.None; level |= AccessLevels.READ_ARTICLES; level |= AccessLevels.READ_COMMENTS;
И чтобы удалить, к примеру, возможность чтение комментариев, воспользуемся XOR:
level = level ^ AccessLevels.READ_COMMENTS; // или level ^= AccessLevels.READ_COMMENTS;
Для того, чтобы проверить включен ли нужный нам флаг — используем следующую конструкцию из логического И и сравнения:
bool b = (level & AccessLevels.READ_ARTICLES) == READ_ARTICLES; // или для последних версий .NET Framework и всех версий .NET Core можно использовать метод Enum.HasFlag: bool b = level.HasFlag(AccessLevels.READ_ARTICLES);
Все эти операции (добавить, проверить, удалить) для наглядности и тренировки можно завернуть в специальный враппер-оболочку, чтобы абстрагировать нашу работу с AccessLevels и получить более высокоуровневый подход. Создадим класс BitOperations:
public class BitOperations
{
public AccessLevels Value { get; private set; }
public BitOperations() => this.Value = AccessLevels.None;
public BitOperations(AccessLevels value) => this.Value = value;
public void Add(AccessLevels value) => this.Value |= value;
public void Remove(AccessLevels value) => this.Value ^= value;
public bool Contains(AccessLevels value) => (this.Value & value) == value;
public override string ToString() => this.Value.ToString("G");
}
Как видно из кода, здесь мы реализовали всё те же методы — добавления, удаления или проверки наших доступов. Под капотом такая конструкция оперирует всё теми же битами у перечисления, которое определено как свойство Value, а в остальном — всё то же самое.
Данный код вы можете найти в моём «блогерском» репозитории здесь.
Дополнительно
Для тренировки и самоконтроля битовых калькуляций можно использовать разнообразные бесплатные инструменты. К примеру, в онлайне есть прекрасный инструмент bitwisecmd, которые позволяет проводить любые битовые операции над числами (AND, OR, XOR, битовые смещения и т.д.). А также, вы можете посмотреть мой старый проект BitJuggling на GitHub, который позволяет делать всё то же самое, но только как стандартное приложение Windows:
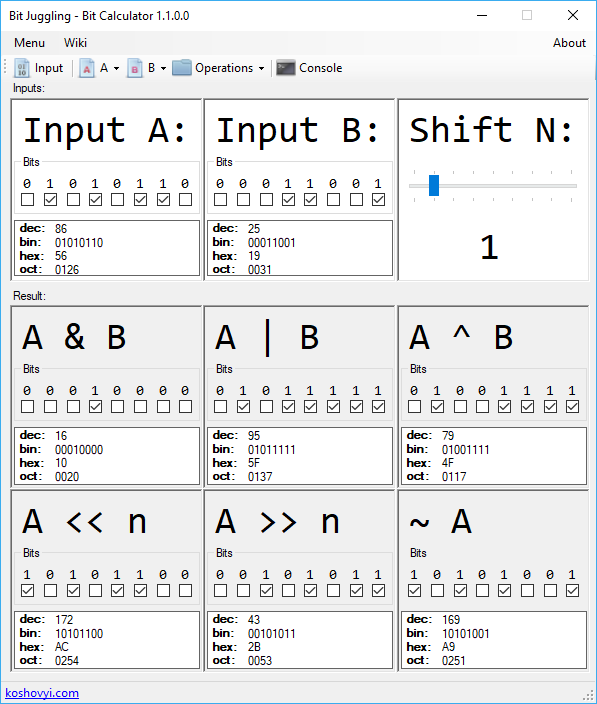
Выводы
Надеюсь, что данная статья поможет вам разобраться или вспомнить о битовых операциях, тонкостях работы и использования. Порой этот простой и невероятно быстрый способ может очень сильно облегчить жизнь и решить сложные и объёмные вещи — малой кровью. Спасибо за чтение, жду ваших комментариев и хорошего вам времени суток! 🙂
